Apr 10, 202253. According to the World Bank, at the end of 2013 \((t=0)\) the U.S. population was 316 million and was increasing according to the following model below where P is measured in millions of people and t is measured in years after 2013. \(P(t)=316e^0.0074t\), a. Based on this model, what will be the population of the United States in 2020? b.
SOLVED: 13.A population of wolves is modeled by the function P and grows according t0 the logistic differential equation dP P SP where is the time in years and P(O) = 100.
For the following exercises, use this scenario: The population P of an endangered species habitat for wolves is modeled by the function P (x)=\frac 558 1+54.8 e^ -0.462 x, P (x) = 1+54.8e−0.462×558, where x is given in years. Graph the population model to show the population over a span of 10 years. Solution Verified

Source Image: researchgate.net
Download Image
The population of a species that grows exponentially over time can be modeled by P (t)=Pe^ (kt), where P (t) is the population after time t, P is the original population when t=0, and k is the growth constant.

Source Image: chegg.com
Download Image
An individual-based model to explore the impacts of lesser-known social dynamics on wolf populations – ScienceDirect For the following exercises, use this scenario: The population P P of an endangered species habitat for wolves is modeled by the function P(x) = 558 1+54.8e−0.462x, P ( x) = 558 1 + 54.8 e − 0.462 x, where x x is given in years. Graph the population model to show the population over a span of 10 years.
Source Image: janpowell.weebly.com
Download Image
A Population Of Wolves Is Modeled By The Function P
For the following exercises, use this scenario: The population P P of an endangered species habitat for wolves is modeled by the function P(x) = 558 1+54.8e−0.462x, P ( x) = 558 1 + 54.8 e − 0.462 x, where x x is given in years. Graph the population model to show the population over a span of 10 years. To model population growth using a differential equation, we first need to introduce some variables and relevant terms. The variable \(t\). will represent time. … be a real number that represents the growth rate. The function \(P(t)\) represents the population of this organism as a function of time \(t\), and the constant \(P_0\) represents
Untitled
Calculus Calculus questions and answers 15. A population of wolves is modeled by the function P and grows according to the logistic differential equation :), where t is the time in years and P (0) = 1500. Which of = 8P (1 – %3D %3D 8000 the following statements are false? Melanism and Wolves – The Wolf Intelligencer

Source Image: thewolfintelligencer.com
Download Image
Solved] A population of wolves is modeled by the function P and grows… | Course Hero Calculus Calculus questions and answers 15. A population of wolves is modeled by the function P and grows according to the logistic differential equation :), where t is the time in years and P (0) = 1500. Which of = 8P (1 – %3D %3D 8000 the following statements are false?
Source Image: coursehero.com
Download Image
SOLVED: 13.A population of wolves is modeled by the function P and grows according t0 the logistic differential equation dP P SP where is the time in years and P(O) = 100. Apr 10, 202253. According to the World Bank, at the end of 2013 \((t=0)\) the U.S. population was 316 million and was increasing according to the following model below where P is measured in millions of people and t is measured in years after 2013. \(P(t)=316e^0.0074t\), a. Based on this model, what will be the population of the United States in 2020? b.

Source Image: numerade.com
Download Image
An individual-based model to explore the impacts of lesser-known social dynamics on wolf populations – ScienceDirect The population of a species that grows exponentially over time can be modeled by P (t)=Pe^ (kt), where P (t) is the population after time t, P is the original population when t=0, and k is the growth constant.

Source Image: sciencedirect.com
Download Image
Pin by Nikki Aldrich on hayden | Werewolf aesthetic, Werewolf stories, Werewolf name A population of wolves is modeled by the function P and grows according to the logistic differential equation dP/dt=5P (1- (P/5000)) where t is the time in years and P (0) = 1000. Which of the following statements are true? limt→∞P (t)=5000 dP/dt is positive for t>0 d2P/dt2 is positive for t>

Source Image: pinterest.com
Download Image
Solved] A population of wolves is modeled by the function P and grows… | Course Hero For the following exercises, use this scenario: The population P P of an endangered species habitat for wolves is modeled by the function P(x) = 558 1+54.8e−0.462x, P ( x) = 558 1 + 54.8 e − 0.462 x, where x x is given in years. Graph the population model to show the population over a span of 10 years.
Source Image: coursehero.com
Download Image
Examples: Exponential Growth – Math1375 – Ganguli – Fall 2020 To model population growth using a differential equation, we first need to introduce some variables and relevant terms. The variable \(t\). will represent time. … be a real number that represents the growth rate. The function \(P(t)\) represents the population of this organism as a function of time \(t\), and the constant \(P_0\) represents
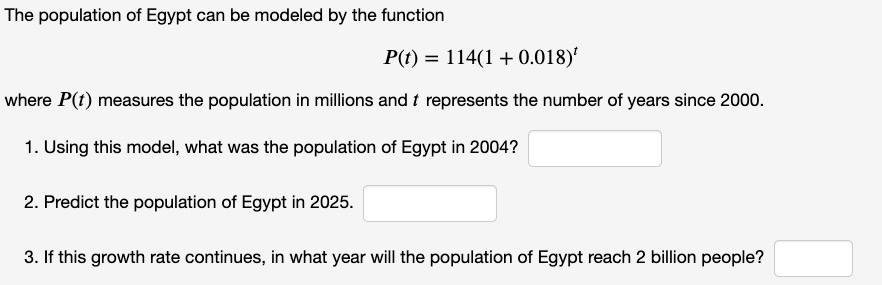
Source Image: openlab.citytech.cuny.edu
Download Image
Solved] A population of wolves is modeled by the function P and grows… | Course Hero
Examples: Exponential Growth – Math1375 – Ganguli – Fall 2020 For the following exercises, use this scenario: The population P of an endangered species habitat for wolves is modeled by the function P (x)=\frac 558 1+54.8 e^ -0.462 x, P (x) = 1+54.8e−0.462×558, where x is given in years. Graph the population model to show the population over a span of 10 years. Solution Verified
An individual-based model to explore the impacts of lesser-known social dynamics on wolf populations – ScienceDirect Solved] A population of wolves is modeled by the function P and grows… | Course Hero A population of wolves is modeled by the function P and grows according to the logistic differential equation dP/dt=5P (1- (P/5000)) where t is the time in years and P (0) = 1000. Which of the following statements are true? limt→∞P (t)=5000 dP/dt is positive for t>0 d2P/dt2 is positive for t>